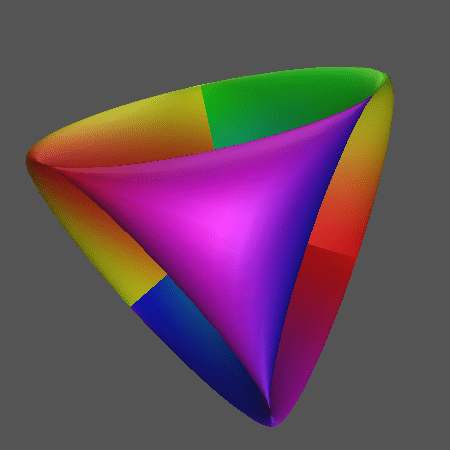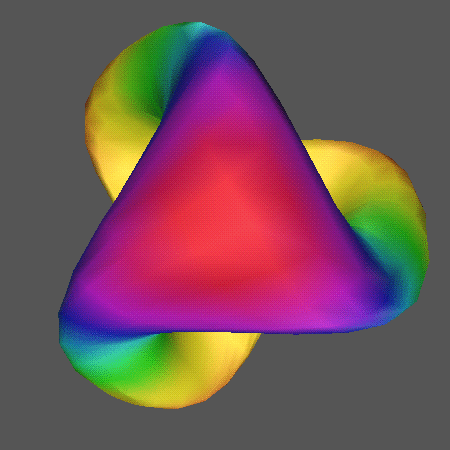The Math of Non-Orientable Surfaces

Preface for Teachers 
1. Introduction to Orientability:  A Fable 
2. The Math of Non-Orientable Surfaces 
1. Surface and Manifold
2. Non-Orientable Surface 
3. Orientable Surfaces:  Sphere, Torus
4. Möbius Band
5. Klein Bottle 
6. Real Projective Plane 
7. And Beyond: 3-Manifolds 
8. What Would it Be Like to Live on a...?
9. Homework Exercises about Math
3. The History and Philosophy of Non-Orientability 
1. The Original Topological Tyrant
2. Klein Bottles and Kant
3. Homework Exercises about History and Philosophy
4. Literature 
1. "The No-Sided Professor"
2. "A Subway Named Moebius"
3. Extra Short Stories
4. The Bald Soprano
5. The Gift
6. Homework Exercises about Literature
5. Music
1. Bach and Schoenberg
2. The Moebius Strip Tease
3. If You're Musically Inclined...
4. Homework Exercises about Music
6. Other Topics 
1. Knit Hats and Scarves
2. Fun Toys on the Internet
3. Non-Orientable Housing
4. The Marvelous Moebius Molecule
5. Moebius Mistakes
6. Non-Orientable Surfaces in Art
7. Homework Exercises on These Topics
7. Bibliography 

Basically, a manifold is a shape.  When we think of shapes we normally think about circles or squares or triangles, but we want our definition of a shape to be more broad.  After all, almost anything you can imagine has a shape, even though that shape may not have a specific name.  Shapes may also have different dimensions.  For example, a square has two dimensions, height and width, and a cube has three dimensions, height, width, and depth, but clearly both are shapes.  Thus a one-dimensional manifold (or one-manifold) is just a one-dimensional shape or a curve.  A two-dimensional manifold (or two-manifold) is just a two dimensional shape or a surface. 

Now the following question may have popped up in your head: “Wait a minute!  A circle is a curve.  But I need two dimensions to draw a circle, so how can a circle be a one-manifold?” 

This is a very good question indeed.  However, when I say that a manifold is one-dimensional, I only mean that each tiny section of the manifold looks like a line.  Mathematicians would say that a one-manifold has the local topology of a line.  Likewise, a two-manifold has the local topology of a plane.  A three-manifold has the local topology of three-dimensional space.  This may still seem a little confusing but the following example may help: Let’s say that the earth was completely smooth (no mountains, hills, craters, buildings, etc.).  In other words, consider the earth as a perfect sphere.  Now imagine yourself walking on the earth.  How do you know it is a sphere?  You know the earth is a sphere because scientists have proved by numerous experiments that it is a sphere.  However, from where you are standing the earth probably looks mighty flat.  In other words, locally the earth is flat.  This is what we mean when we say that a sphere (remember that a sphere is only a surface, it is not a solid ball) or any other two-manifold has the local topology of a plane. 

Consider the sphere.  Clearly this surface has no mirror-reversing effect because nobody on earth has ever returned mirror-reversed after a long journey.   (A mirror-reversed person would seem to have changed handedness and would see all of our writing backwards).  So presumably a sphere is orientable.  The sphere also has some nice properties.  You can walk in any direction on the sphere and you will end up where you started.  This also means that you cannot fall off of the sphere (this is especially convenient for those of us who live on the earth).  When a surface or any manifold has these properties, we say that the manifold has no boundary.  But isn’t the sphere itself a boundary for the space it encloses?  Remember that when we talk about two-manifolds we are only considering the surface itself.  For all we know, the space that a sphere encloses does not even exist.  Imagine that you are a two-dimensional being living in the surface of the sphere.  (Those of you who have read Flatland by Edwin Abbott Abbott should have no trouble visualizing this.)  You have no conception of the three-space that might exist outside of your world.  Your entire world simply looks like one infinite plane.  Therefore, a two-dimensional being living in the surface of the sphere would truly believe that his world had no boundary, even though it has a finite area. 

Let’s now consider another orientable surface, the torus.  We usually think of a doughnut in association with a torus, but the following picture is also a torus: 

We call this a flat torus for obvious reasons.  Although it does not look like a torus, it contains the instructions for building a torus.  Notice that if we glue the sides with corresponding arrows together, we will end up with a doughnut shape.  If we keep in mind that when you go off each side of the flat torus you return at the same spot on the opposite side, the flat torus will have the same properties as the folded torus.  In other words, the flat torus has the same topology as the folded torus.  For our purposes, it will be much easier to consider the flat torus than the folded torus, so from now on when we say “torus”, we mean “flat torus”. 

Like the sphere, the torus has no boundary.  When we go off an edge, we return on the opposite side, so it is impossible to leave the surface.  What would we have if we changed the torus so that you could not go off the top or the bottom of the surface?  Well, now we glue only the left and right sides together so we get a cylinder.  Since we are blocked off if we try to go off the top or the bottom, the cylinder does have a boundary.  In fact it has two boundaries, one for the top and one for the bottom.  This distinction will become important in a moment. 

Here's a model of a folded torus you can play around with, so you can get an idea of an orientable surface.  Use your mouse to rotate the object. 
 

 But now let’s change our  torus diagram  to look like this: 

Notice that now the left and right sides of this surface are connected with a twist.  If I leave the box towards the top of the left edge, I will return towards the bottom of the right edge.  Furthermore, I will be mirror-reversed.  Although I am facing the same way I was before (I am still facing the left edge), the hand that was formerly my left hand is now my right hand and vice versa.  Thus we have found our first nonorientable surface! 

(Remember, when we talk of travelling in a surface, we're talking about travelling inside the surface, not on top of it.  Imagine it as an infinitely flat animal travelling on a sphere; essentially, she's travelling in the surface.  In contrast, when we walk on a sphere, we're walking on it; unlike our flat friend, we can imagine moving up and down perpendicular to the ground.) 

The surface we have just discovered is called a Moebius strip.  And the best thing about a Mobius strip is that we can actually build it.  (We will soon see that most nonorientable surfaces cannot be built in three-space).  It’s easy to build.  Just take a strip of paper and attach the ends with a single twist.  You should end up with something like the following picture: 
 
 

The Moebius strip (also sometimes called a Mobius band) has a boundary just like the cylinder, but it only has one boundary, not two.  If you trace along the edge of the Mobius strip you just built, you will cover the entire boundary, eventually returning to the place where you started.

Now that we have discovered one nonorientable surface we can create many more.  In fact, any surface (or any manifold at all) which has a Moebius band in its structure is nonorientable.  The following example may help convince you.  Here are the instructions for our next surface: 

This surface is similar to the Moebius strip except that now the top and bottom are glued together as they were in the torus.  Likewise, we could also think of this surface as a torus with a Moebius strip in it.  However, if you try to build this surface you will find that it is impossible.  As it turns out, you cannot build this surface in three-space without having it intersect itself.  If we lived in the fourth dimension, we could build it. 

This new surface is called a Klein bottle.  Although the Klein bottle cannot be built in three-space, we can project it into three-space from four-space using computers.  In fact, as long as we are content to have it intersect itself, we can even make three-dimensional models of those projections. Here are two different projections of the Klein bottle generated by computers: 
 

The Klein bottle has a mirror reversing effect just like the Moebius strip, but it also has the nice property of having no boundary so you can go off what looks to be the edge in the diagram without ever really coming to the edge. 

We will consider one last nonorientable surface before moving onto three-manifolds.  The surface is called the real projective plane (or just projective plane) and it can be constructed in a variety of ways.  One way to think about it is to take the flat Klein bottle diagram and connect the top and bottom edges with a twist in addition to the left and right edges: 

Another way to model the projective plane is to start with a hemisphere and connect each point on the rim to its corresponding point on the opposite side with a twist.  Here is a picture of what we mean by this: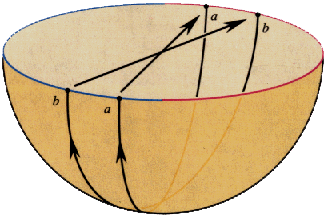 

Like the Klein bottle, the projective plane has no boundary and cannot be built in three-space without self-intersection.  Here are a few computer images of projective planes embedded in three-space.  You can click on the picture to learn some more about each projection from the Geometry Center: 
 
 

The Crosscap	The Roman Surface	Boy's Surface

Consider a solid cube.  (It is important to stress that the cube is solid or that we are talking about the space inside of the cube and not just the cubical surface).  The cube itself is a three-manifold with a boundary on all sides.  However, it is a pretty boring space.  What if we connected the right wall to the left wall?  Then when you walked through the right wall, you would return to the cube through the left wall.   Better yet, you could play catch with yourself.  Just throw a ball towards the right wall, turn around, and catch it as it comes through the left wall.  We could also connect the front wall to the back wall and the top wall to the bottom wall.  This new manifold is called a three-torus. 

The three-torus has no boundary and therefore if you lived in a three-torus it would seem to be an infinite space.  In theory our universe could be a three-torus.  If this were the case, if you looked out in any direction far enough you would see yourself (ignoring the fact that light travels at a finite speed).  Of course, we cannot build a three-torus in three-space, just as we can’t build a regular folded torus in the plane.  More generally, a manifold without boundary, which is not infinite, cannot be built in the same dimension that its local topology consists of. 

What if we wanted to create a nonorientable three-manifold?  How would we do it?  In two dimensions we connected the edges of a rectangle with a flip.  We can do the same in three dimensions.  In fact there are two ways to cause a mirror reversing effect.  We could connect opposite faces of the cube with a side-to-side flip or an upside-down flip.  Let’s say we connected the front and back walls of our cube with a side-to-side flip.  Now, when you walked out the right side of the back wall, you would return on the left side of the front wall.  You would also be mirror-reversed.  What if we connected the front and back walls with an upside-down flip?  Then, if you left the back wall standing on the floor, you would return through the front wall hanging from the ceiling (this,of course, ignores gravity).  Again, you would also return mirror-reversed.  Naturally we could connect each pair of opposite walls with a flip of either sort making for an extremely confusing space to live in.  As an exercise, imagine connecting the walls of the cube in various ways, and then determine how you would return after leaving the cube through one of the faces. 

Now you may be wondering what would happen if we connected a pair of opposite walls with both a side-to-side flip and an upside-down flip.  The interesting thing is that you would not return mirror-reversed at all.  This is because if you get mirror-reversed twice you will return to normal.  However, you will have made a 180 degree turn (you will be upside down, but your right hand will still be on your right side). 

Thus far we have only discussed connecting the opposite sides of our fundamental domains, but there is no reason that we could not connect the front wall of our cube to the right wall.  As you can see, this would open up numerous other possibilities for the shapes of manifolds.  There is in fact such a thing as projective three-space that has similar properties to the projective plane. 
 

First, a two dimensional creature living in a Moebius strip.  Notice how the colors switch position when the creature gets flipped. 

Next, the same two dimensional creature living on a Klein bottle.  This time, the colors get flipped only if the creature goes off to the sides; it just comes around without flipping if it goes off the top or the bottom. 

Finally, a slightly different example.  This ball is on a real projective plane. The changing colors symbolize a switch in orientation. Watch how the ball changes orientation regardless of which edge it goes off. 

• Play a game of tic-tac-toe with a partner on each of the three surfaces described.
• Come up with a game you think would be interesting to play on one of the surfaces.  Write a discription of the game and play a round.
• Create your own 3-manifold by twisting its fundamental domain in an interesting way.  Come up with a name for your manifold and write a discription of what it would be like to live in the manifold.
• Write a creative story about flat creatures living on the surface of a non-orientable manifold.

Thanks to Eric Weisstein who created the Mathematica files that you can rotate on this page.  The picture of a hemisphere representation of the projective plane was scanned from Beyond the Third Dimension p.188.  The three images of projective planes are from the Geometry Center's Topological Zoo.  The "crab" applets were written by Zbigniew Fiedorowicz and the the animated .gif of a ball was created by Joe Fields. 

For further reading, look at the following books: 

Abbott, Edwin Abbott.  Flatland.  New York:  Dover, 1992.  [Also online.] 

Carter, J. Scott.  How Surfaces Intersect in Space.  New Jersey:  World Scientific, 1993. 

Weeks, Jeffery R.  The Shape of Space.  New York:  M. Dekker, 1985. [This book discuss especially well the material in this chapter.] 

On the web, you can look at the following sites: 

CRC Concise Encyclopedia of Mathematics.  (Due to copyright issues, certain pages are blocked on different days.) 

Paul Bourke's site on geometry. 

The Geometry Center's 
Topological Zoo. 

Jeff Weeks has the rough draft of a  a series of exercises for middle-schoolers based on his The Shape of Space at the Geometry Center's page.  He also has some nifty games using the flat torus and the flat Klein bottle. 

For more information on sources and other ideas for further reading, see the bibliography.