Literature

Click on the Chapter or Subchapter you wish to read.

Introduction

The great thing about non-orientable surfaces, and Moebius bands in particular, is their omnipresence. We guarantee you that by the time you have gone through this unit on non-orientable surfaces, you will see Klein bottles and Moebius strips everywhere. At least, that’s what happened to us. You have by now gotten a glimpse of the mathematics of non-orientable surfaces, and if you are confused about how to apply the mathematics to other areas, we suggest that you keep the following phrase in mind: a Moebius band is a loop with a twist. In other words, when you find a situation where you have come back to step one with a twist, it is shaped as a Moebius strip .

We found several examples in literature where the subject of the narrative is non-orientables surfaces (mainly Moebius strips), or where the narrative itself takes the shape of a moebius strip. The most accessible are the first, and the two we chose to include in our course are “The No-sided Professor,” by Martin Gardner, and “A Subway Named Moebius,” by A.J. Deutsch. They can both be found in the collection of short stories called Fantasia Mathematica, assembled by Clifton Fadiman. cover of Fantasia Mathematica We also found two examples of works where the plot resembled a Moebius strip--Ionesco’s play The Bald Soprano and Nabokov’s novel The Gift. The Bald Soprano is very accessible too--it is an easy read, and the Moebius strip analogy is straightforward. The Gift, on the other hand, is more obscure, and we suggest that only the more advanced readers try to tackle it.

We hope that the examples of Moebius strip literature we chose will inspire you to create your own short stories, poems, etc. Also, our selection is by no means exhaustive--take a minute to think of other books you have already read which remind you of non-orientable surfaces!

“The No-sided Professor” by Martin Gardner

What happens when the Moebius Society, a small, obscure Chicago organization of mathematicians working in the field of topology, gets together for its annual banquet, held for the first time at Chicago’s Purple Hat Club, with special guest Dr. Stanislav Slapernarski, who promises to speak on the topic of the no-sided surface? Understanding that a surface like a Moebius strip has only one side is already a big step to take. Martin Gardner, in “The No-sided Professor”, goes one step further, by introducing the possibility of a no-sided surface.

The writing is straight-forward--so go ahead and enjoy the read! Here are just a few questions for you to keep in mind as you go through the tale.

Why does Gardner start the story like he did? After all, the first few paragraphs hardly seem to be related to math. Think also of the reasons he might have had for starting with the end of plot, and then doing a flashback to the beginning.
How does Gardner introduce mathematical notions into his tale? How does he define topology, and how does he describe a Moebius strip? Did you find his explanations accessible? To simple, too difficult? Is Gardner's story just funny, or can we draw some mathematical information from it? If so, what?
How successful is his presentation of a no-sided surface made out of paper? Were you satisfied with the explanation? Do you think it was meant to be mathematically accurate, or more of a diversion?
Why did the professors have to enter a higher dimension when they turned into “no-sided” people? Keep in mind the Klein bottle and the projective plane.
Explain why the Klein bottle cups were able to hold liquid, even though there is no inside and no outside.
Can you think of a real mathematical reason that Simpson and Slapenarski could have been turned inside out? Or is this just a narrativedevice by Garner to make the end of the story more interesting?
Rewrite the ending.

“A Subway Named Moebius” by A. J. Deutsch

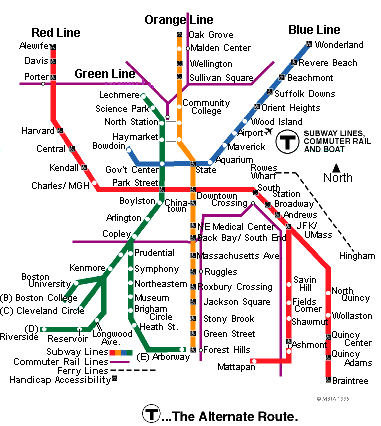Crisis in the Boston subway system! Thanks to the Boylston shuttle, which tied together the seven principle lines on four different levels, a train could get from one station in the system to any other. Deutsch’s tale is an attempt to explain singularities, Moebius bands and Klein bottles by placing them in a “real life situation.” Of course, the tale is confusing at times--by virtue of dealing with concepts which are foreign to living in the 3rd dimension, we have some trouble assimilating the ideas. However, with the background in math which you already covered in this chapter, you will at least be familiar with what Deutsch is trying to explain.

How does Deutsch define the following mathematical concepts: a node, a singularity?
How is does the conclusion of the story resemble a Moebius strip?
Why is it important to keep the Boylston shuttle in the system?
What happens to time in the missing subway 86?

The Bald Soprano by Eugene Ionesco

The Bald Soprano has very little narrative similarity with the two short stories we suggested that you read as an introduction to literature and non-orientable surfaces. The tales are excuses to get mathematical concepts across to a general public--the mathematics comes before the literature, and both authors were above all mathematicians. This is not the case for Ionesco’s play. Ionesco was a writer, and his works are not known for their mathematical content. In fact, most spectators and readers of his plays are probably unaware that when they see or read The Bald Soprano, they are actually witnessing a great example of Moebius literature. In fact, there is no evidence that Ionesco himself was aware that the narrative twist he gave to the conclusion of his play imitated a Moebius strip.

Eugene Ionesco The play is an easy read. Mr. and Mrs. Smith invite Mr. and Mrs. Martin over for dinner, and conversation gradually gets completely out of hand, until there seems to be no more logical connection between the characters’ responses, as though Ionesco were taking random phrases and placing them one after the other. " Theater of the absurd" is one of the phrases most commonly ascribed to Ionesco. We are thoroughly lost by the last pages of the play, and are unable to make any more logical links in the plot, until the concluding stage directions, which read: “Mr. and Mrs. Martin are sitting like the Smiths at the beginning of the play. The play starts again with the Martins, who are saying exactly the same words as the Smiths in the first scene.” (In fact, there have been productions in which the play has been performed for 24 hours straight, switching continuously from the Smiths to the Martins.) It’s a loop with a twist situation. The play has started over again, and the only difference is that the characters have been switched around.

We know that Ionesco made a conscious effort to portray an absurd situation in his play, yet we do not know whether he was conscious of the Moebius narrative shape his work took on.

What does this say about the relation between Moebius strips and the absurd?
Is a Moebius strip an absurd situation? Is Ionesco’s play not as absurd as he would have liked it to come across?
As you read the play, think about the connection between what is an mathematical example of a non-orientable surface, and a real life situation.
For those of you who have always had an aversion to mathematics, does this literary illustration of a Moebius strip, which seems to have been created without any mathematical forethought, help you see how math can appear “naturally”?

The Gift by Vladamir Nabokov

Vladimir Nabokov’s The Gift is by far my favorite literary example of a Moebius strip of the ones we came up with. It is also by far the most difficult one to come to terms with, and let me suggest that only more advanced readers try working on it. Whereas it is easy to skim through Ionesco’s The Bald Soprano and find a loop with a twist, sitting down with The Gift is a much more lengthy task. Nabokov’s style is incredibly rich—every single phrase overflows with meaning, with images begging to be unloaded and interpreted—so I suggest you undertake the challenge only if you have a considerable amount of time ahead of you. I do not mean to deter you from an exploration of The Gift. On the contrary, I want you to be fully prepared and conscious of intensity of Nabokov’s work.

Nabokov’s work is full of mathematical references. In fact, one of the first sentences of The Gift reads thus: “Running along [the van’s] entire side was the name of the moving company in yard-high blue letters, each of which (including a square dot) was shaded laterally with black paint: a dishonest attempt to climb into the next dimension.” The author alludes to geometrical configurations and to distortions of space and time throughout his book, so it is no surprise to find Moebius metaphors in it as well. I see the Moebius motif appear in two different ways, but before I develop them, let me briefly summarize the plot of the novel.

Fyodor is a young, hitherto unknown writer who has just published his first collection of poems, and Chapter One of The Gift centers around this first publication. Chapter Two then moves on to describe Fyodor’s progress as a writer, and also discusses Fyodor’s father’s zoological explorations. This chapter is largely centered around how Pushkin is reflected in Fyodor’s work, and Chapter Three Vladamir Nabokov [Corbis] concentrates on Gogol’s influence. By this time, Fyodor has met Zina, who encourages and supports him as he writes a literary biography of Chernyshevski. Chapter Four is the actual book which Fyodor writes. The last chapter comes back to an older Fyodor, who sketches out the book he wishes to write: The Gift. As you can tell from this summary, or from having read the book yourself, the narrative is very intertwined. One plot line emerges from another, until you have lost track of where to find the “true” narrative. Nabokov himself called Chapter four, the book within a book, a “spiral within a sonnet”—quite a beautiful image to portray the narrative twists in The Gift.

I suggested earlier on that if you ever got confused as to how literature could imitate a Moebius strip, you could think: “a loop with a twist”. If you extend this image, you can also think to yourself: “if you follow the Moebius strip around, what was once the inside becomes the outside, and what was once the outside becomes the inside.” This image applies directly to the narrative structure of The Gift. Fyodor is on the inside of the narrative at the beginning of the work: he is a character who Nabokov, author of The Gift, is writing about, describing his beginnings as a writer, and how he comes to meet his girlfriend Zina. Once we get to the final chapter, however, Fyodor discusses with Zina the book he wants to write: “Here is what I’d like to do,” he said. “Something similar to destiny’s work in regard to us. Think how fate started it three and a half odd years ago…” From there, Fyodor proceeds to explain that he wants to write a book about exactly what we just read: his emergence as a writer and the gradual evolution of his relationship with Zina. Fyodor is no longer the character of Nabokov’s The Gift, but the author of his own The Gift. He is now on the outside! This is really quite a remarkable yet subtle narrative twist.

Was Nabokov aware that his book imitated a Moebius strip? There is no evidence that he was—none of his comments on The Gift suggest it. In fact, the inventor of the Moebius metaphor in The Gift seems to be Omry Ronen, who used to be a literature professor at Yale and is now at University of Michigan. One of his students when he taught at Yale, Serguei Davidov, picked up on the metaphor and developed it extensively. Apparently, Ronen was very possessive of his metaphor, and one day, upon presenting his student Davidov with a present, signed it "from the author of the Moebius strip metaphor," to stress the fact that although Davidov discussed the image later, it originated from Ronen.

From a formal point of view of the narrative, therefore, The Gift imitates a Moebius strip. Furthermore, if we examine the language of The Gift, there are a number of moments which relate to Moebius strips also. The idea of flips and twists comes up often: "at the end, there is always one that does a kind of flip, and then hastily assumes its position," says the narrator about a commercial. "I turn my life inside down so that birth becomes death, I fail to see at the verge of this dying-in-reverse anything that would correspond to the boundless terror that even a centenarian is said to experience when he faces the positive end," he says further on. Or still later on in the narrative: "you look at a person and you see him as clearly as if he were fashioned of glass and you were the glass blower, while at the same time without in the least impinging upon the clarity you notice some trifle on the side--such as the similarity of the telephone receiver's shadow to a jug, slightly crushed ant, and (all this simultaneously) the convergence is joined by a third thought--the memory of a sunny evening at a Russian small railway station; ie. images having no rational connection with the conversation you are carrying on while your mind runs around the outside of our own words and along the inside of those of your interlocutor." Once again, we find the inside/outside image.

As you read, try to keep in mind the inside/outside metaphor.
How many times do those terms come up together in the novel?
What other images also remind you of the Moebius strips in the novel?

For homework, answer the questions posed to the right on the following works:

"The No-sided Professor"
"A Subway Named Moebius"
The Bald Soprano
The Gift

If you have extra time or want to pursue this further, look at the extra short stories we recomend.

In his introduction to Fantasia Mathematica, editor Clifton Fadiman writes: "The reader will note that several of the stories base themselves upon our old friend, the Moebius strip. It is remarkable how many narrative variations are possible using only this particular device; I have in my files half a dozen other Moebius strip stories. . . " What about the Moebius band, do you think, inspires so many stories? What makes it so compelling to write about?
There's an Argentine film from 1996 called Moebius that has a similar plot to "A Subway Named Moebius." Watch the movie and compare and contrast the two stories.

This section written by MLB.

The picture of the cover of Fantasia Mathematica is from Amazon. The Boston T map comes from the MBTA website. The picture of two people trying to paint a Moebius band is from Zbigniew Fiedorowicz's Introduction to Toplogy site. Eugene Ionesco's photograph comes from the Romanian American Forum's list of famous Romanians. The picture of Nabokov is from Corbis. Thanks to Professor Vladamir Alexandrov of the Yale Department of Slavic Language and Literature for his help with The Gift.

For further reading, look at the following books:

Fadiman, Clifton. Fantasia Mathematica. New York: Simon and Schuster, 1958. (Republished in 1997 by Springer-Verlag).

Ionesco, Eugene. "The Bald Soprano." In The Bald Soprano and Other Plays, Donald M. Allen, translator. Grove Press, 1982.

Nabokov, Vladimir. The Gift. New York: Vintage, 1991.

On the web, you can look at the following sites:

Søren Olsen's biography of Eugene Ionesco.

Zembla, a site devoted to all things Nabakov.

There are two sites on the movie "Moebius:" one from the film's creators and one from the Internet Movie Database.

For more information on sources and other ideas for further reading, see the bibliography.